Unit - I
Part - 4
Continue in Greedy Algorithm
Definition: Merge n sorted sequences of different lengths into one output while minimizing reads. Only two sequences can be merged at once. At each step, the two shortest sequences are merged.
Formal Definition: Let D={n1, ... , nk} be the set of lengths of sequences to be merged. Take the two shortest sequences, ni, nj∈ D, such that n≥ ni and n≥ nj ∀ n∈ D. Merge these two sequences. The new set D is D' = (D - {ni, nj}) ∪ {ni+nj}. Repeat until there is only one sequence.
See also simple merge, ideal merge, Huffman coding, greedy algorithm.
Note: Merging sequences by length is the same as joining trees by frequency in Huffman coding. For example, let there be a set of sorted sequences of the following lengths: D={3,5,7,9,12,14,15,17}. Building the optimal merge tree goes as follows. Note that merged sequences are replaced by the sum of their lengths. For instance, the first step merges the sequence of length 3 and the sequence of length 5 to get a sequence of length 8.
Part - 4
Continue in Greedy Algorithm
optimal merge
(algorithm)Definition: Merge n sorted sequences of different lengths into one output while minimizing reads. Only two sequences can be merged at once. At each step, the two shortest sequences are merged.
Formal Definition: Let D={n1, ... , nk} be the set of lengths of sequences to be merged. Take the two shortest sequences, ni, nj∈ D, such that n≥ ni and n≥ nj ∀ n∈ D. Merge these two sequences. The new set D is D' = (D - {ni, nj}) ∪ {ni+nj}. Repeat until there is only one sequence.
See also simple merge, ideal merge, Huffman coding, greedy algorithm.
Note: Merging sequences by length is the same as joining trees by frequency in Huffman coding. For example, let there be a set of sorted sequences of the following lengths: D={3,5,7,9,12,14,15,17}. Building the optimal merge tree goes as follows. Note that merged sequences are replaced by the sum of their lengths. For instance, the first step merges the sequence of length 3 and the sequence of length 5 to get a sequence of length 8.
3 5 7 9 12 14 15 17
8 7 9 12 14 15 17 / \ 3 5
15 9 12 14 15 17
/ \
8 7
/ \
3 5
15 21 14 15 17
/ \ / \
8 7 9 12
/ \
3 5
29 21 15 17
/ \ / \
14 15 9 12
/ \
8 7
/ \
3 5
29 21 32
/ \ / \ / \
14 15 9 12 15 17
/ \
8 7
/ \
3 5
50 32
/ \ / \
/ \ 15 17
29 21
/ \ / \
14 15 9 12
/ \
8 7
/ \
3 5
82
/ \
/ \
/ \
50 32
/ \ / \
/ \ 15 17
29 21
/ \ / \
14 15 9 12
/ \
8 7
/ \
3 5
[https://xlinux.nist.gov/dads/HTML/optimalMerge.html]
Optimal Merge Patterns
- Input: N sorted arrays of length L[1], L[2],...,L[n]
- Problem: Ultimateley, to merge the arrays pairwise as fast as possible. The problem is to determine which pair to merge everytime.
- Method (the Greedy method): The selection policy (of which best pair of arrays to merge next) is to choose the two shortest remaining arrays.
- Implementation:
- Need a data structure to store the lengths of the arrays, to find the shortest 2 arrays at any time, to delete those lengths, and insert in a new length (for the newly merged array).
- In essence, the data structure has to support delete-min and insert. Clearly, a min-heap is ideal.
- Time complexity of the algorithm: The algorithm iterates (n-1) times. At every iteration two delete-mins and one insert is performed. The 3 operations take O(log n) in each iteration.
- Thus the total time is O(nlog n) for the while loop + O(n) for initial heap construction.
- That is, the total time is O(nlog n).
[https://www.mutah.edu.jo/userhomepages/CS252/greedy.html#2ndapplication]
Minimum spanning tree
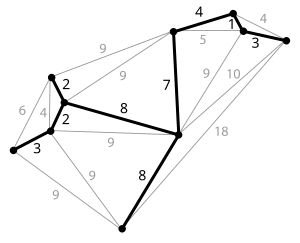
A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. That is, it is a spanning tree whose sum of edge weights is as small as possible. More generally, any undirected graph (not necessarily connected) has a minimum spanning forest, which is a union of the minimum spanning trees for its connected components.
There are quite a few use cases for minimum spanning trees. One example would be a telecommunications company which is trying to lay out cables in new neighborhood. If it is constrained to bury the cable only along certain paths (e.g. along roads), then there would be a graph representing which points are connected by those paths. Some of those paths might be more expensive, because they are longer, or require the cable to be buried deeper; these paths would be represented by edges with larger weights. Currency is an acceptable unit for edge weight – there is no requirement for edge lengths to obey normal rules of geometry such as the triangle inequality. A spanning tree for that graph would be a subset of those paths that has no cycles but still connects to every house; there might be several spanning trees possible. A minimum spanning tree would be one with the lowest total cost, thus would represent the least expensive path for laying the cable.
A planar graph and its minimum spanning tree. Each edge is labeled with its weight, which here is roughly proportional to its length.
[]
Kruskal’s Minimum Spanning Tree Algorithm
What is Minimum Spanning Tree?
Given a connected and undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees. A minimum spanning tree (MST) or minimum weight spanning tree for a weighted, connected and undirected graph is a spanning tree with weight less than or equal to the weight of every other spanning tree. The weight of a spanning tree is the sum of weights given to each edge of the spanning tree.
How many edges does a minimum spanning tree has?
A minimum spanning tree has (V – 1) edges where V is the number of vertices in the given graph.
What are the applications of Minimum Spanning Tree?
See this for applications of MST.
Below are the steps for finding MST using Kruskal’s algorithm
1. Sort all the edges in non-decreasing order of their weight.
2. Pick the smallest edge. Check if it forms a cycle with the spanning tree
formed so far. If cycle is not formed, include this edge. Else, discard it.
3. Repeat step#2 until there are (V-1) edges in the spanning tree.
The step#2 uses Union-Find algorithm to detect cycle. So we recommend to read following post as a prerequisite.
Union-Find Algorithm | Set 1 (Detect Cycle in a Graph)
Union-Find Algorithm | Set 2 (Union By Rank and Path Compression)
The algorithm is a Greedy Algorithm. The Greedy Choice is to pick the smallest weight edge that does not cause a cycle in the MST constructed so far. Let us understand it with an example: Consider the below input graph.
The graph contains 9 vertices and 14 edges. So, the minimum spanning tree formed will be having (9 – 1) = 8 edges.
After sorting:
Weight Src Dest
1 7 6
2 8 2
2 6 5
4 0 1
4 2 5
6 8 6
7 2 3
7 7 8
8 0 7
8 1 2
9 3 4
10 5 4
11 1 7
14 3 5
Now pick all edges one by one from sorted list of edges
1. Pick edge 7-6: No cycle is formed, include it.
2. Pick edge 8-2: No cycle is formed, include it.
3. Pick edge 6-5: No cycle is formed, include it.
4. Pick edge 0-1: No cycle is formed, include it.
5. Pick edge 2-5: No cycle is formed, include it.
6. Pick edge 8-6: Since including this edge results in cycle, discard it.
7. Pick edge 2-3: No cycle is formed, include it.
8. Pick edge 7-8: Since including this edge results in cycle, discard it.
9. Pick edge 0-7: No cycle is formed, include it.
10. Pick edge 1-2: Since including this edge results in cycle, discard it.
11. Pick edge 3-4: No cycle is formed, include it.
Since the number of edges included equals (V – 1), the algorithm stops here.
We strongly recommend you to minimize your browser and try this yourself first.
- C/C++
- Java
- Python
// C++ program for Kruskal's algorithm to find Minimum Spanning Tree
// of a given connected, undirected and weighted graph
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// a structure to represent a weighted edge in graph
struct Edge
{
int src, dest, weight;
};
// a structure to represent a connected, undirected and weighted graph
struct Graph
{
// V-> Number of vertices, E-> Number of edges
int V, E;
// graph is represented as an array of edges. Since the graph is
// undirected, the edge from src to dest is also edge from dest
// to src. Both are counted as 1 edge here.
struct Edge* edge;
};
// Creates a graph with V vertices and E edges
struct Graph* createGraph(int V, int E)
{
struct Graph* graph = (struct Graph*) malloc( sizeof(struct Graph) );
graph->V = V;
graph->E = E;
graph->edge = (struct Edge*) malloc( graph->E * sizeof( struct Edge ) );
return graph;
}
// A structure to represent a subset for union-find
struct subset
{
int parent;
int rank;
};
// A utility function to find set of an element i
// (uses path compression technique)
int find(struct subset subsets[], int i)
{
// find root and make root as parent of i (path compression)
if (subsets[i].parent != i)
subsets[i].parent = find(subsets, subsets[i].parent);
return subsets[i].parent;
}
// A function that does union of two sets of x and y
// (uses union by rank)
void Union(struct subset subsets[], int x, int y)
{
int xroot = find(subsets, x);
int yroot = find(subsets, y);
// Attach smaller rank tree under root of high rank tree
// (Union by Rank)
if (subsets[xroot].rank < subsets[yroot].rank)
subsets[xroot].parent = yroot;
else if (subsets[xroot].rank > subsets[yroot].rank)
subsets[yroot].parent = xroot;
// If ranks are same, then make one as root and increment
// its rank by one
else
{
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
// Compare two edges according to their weights.
// Used in qsort() for sorting an array of edges
int myComp(const void* a, const void* b)
{
struct Edge* a1 = (struct Edge*)a;
struct Edge* b1 = (struct Edge*)b;
return a1->weight > b1->weight;
}
// The main function to construct MST using Kruskal's algorithm
void KruskalMST(struct Graph* graph)
{
int V = graph->V;
struct Edge result[V]; // Tnis will store the resultant MST
int e = 0; // An index variable, used for result[]
int i = 0; // An index variable, used for sorted edges
// Step 1: Sort all the edges in non-decreasing order of their weight
// If we are not allowed to change the given graph, we can create a copy of
// array of edges
qsort(graph->edge, graph->E, sizeof(graph->edge[0]), myComp);
// Allocate memory for creating V ssubsets
struct subset *subsets =
(struct subset*) malloc( V * sizeof(struct subset) );
// Create V subsets with single elements
for (int v = 0; v < V; ++v)
{
subsets[v].parent = v;
subsets[v].rank = 0;
}
// Number of edges to be taken is equal to V-1
while (e < V - 1)
{
// Step 2: Pick the smallest edge. And increment the index
// for next iteration
struct Edge next_edge = graph->edge[i++];
int x = find(subsets, next_edge.src);
int y = find(subsets, next_edge.dest);
// If including this edge does't cause cycle, include it
// in result and increment the index of result for next edge
if (x != y)
{
result[e++] = next_edge;
Union(subsets, x, y);
}
// Else discard the next_edge
}
// print the contents of result[] to display the built MST
printf("Following are the edges in the constructed MST\n");
for (i = 0; i < e; ++i)
printf("%d -- %d == %d\n", result[i].src, result[i].dest,
result[i].weight);
return;
}
// Driver program to test above functions
int main()
{
/* Let us create following weighted graph
10
0--------1
| \ |
6| 5\ |15
| \ |
2--------3
4 */
int V = 4; // Number of vertices in graph
int E = 5; // Number of edges in graph
struct Graph* graph = createGraph(V, E);
// add edge 0-1
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
graph->edge[0].weight = 10;
// add edge 0-2
graph->edge[1].src = 0;
graph->edge[1].dest = 2;
graph->edge[1].weight = 6;
// add edge 0-3
graph->edge[2].src = 0;
graph->edge[2].dest = 3;
graph->edge[2].weight = 5;
// add edge 1-3
graph->edge[3].src = 1;
graph->edge[3].dest = 3;
graph->edge[3].weight = 15;
// add edge 2-3
graph->edge[4].src = 2;
graph->edge[4].dest = 3;
graph->edge[4].weight = 4;
KruskalMST(graph);
return 0;
}
Following are the edges in the constructed MST
2 -- 3 == 4
0 -- 3 == 5
0 -- 1 == 10
Time Complexity: O(ElogE) or O(ElogV). Sorting of edges takes O(ELogE) time. After sorting, we iterate through all edges and apply find-union algorithm. The find and union operations can take atmost O(LogV) time. So overall complexity is O(ELogE + ELogV) time. The value of E can be atmost O(V2), so O(LogV) are O(LogE) same. Therefore, overall time complexity is O(ElogE) or O(ElogV)
[http://www.geeksforgeeks.org/greedy-algorithms-set-2-kruskals-minimum-spanning-tree-mst/]
Prim’s Minimum Spanning Tree (MST))
The set mstSet is initially empty and keys assigned to vertices are {0, INF, INF, INF, INF, INF, INF, INF} where INF indicates infinite. Now pick the vertex with minimum key value. The vertex 0 is picked, include it in mstSet. So mstSet becomes {0}. After including to mstSet, update key values of adjacent vertices. Adjacent vertices of 0 are 1 and 7. The key values of 1 and 7 are updated as 4 and 8. Following subgraph shows vertices and their key values, only the vertices with finite key values are shown. The vertices included in MST are shown in green color.
Pick the vertex with minimum key value and not already included in MST (not in mstSET). The vertex 1 is picked and added to mstSet. So mstSet now becomes {0, 1}. Update the key values of adjacent vertices of 1. The key value of vertex 2 becomes 8.
Pick the vertex with minimum key value and not already included in MST (not in mstSET). We can either pick vertex 7 or vertex 2, let vertex 7 is picked. So mstSet now becomes {0, 1, 7}. Update the key values of adjacent vertices of 7. The key value of vertex 6 and 8 becomes finite (7 and 1 respectively).
Pick the vertex with minimum key value and not already included in MST (not in mstSET). Vertex 6 is picked. So mstSet now becomes {0, 1, 7, 6}. Update the key values of adjacent vertices of 6. The key value of vertex 5 and 8 are updated.
We repeat the above steps until mstSet includes all vertices of given graph. Finally, we get the following graph.
How to implement the above algorithm?
We use a boolean array mstSet[] to represent the set of vertices included in MST. If a value mstSet[v] is true, then vertex v is included in MST, otherwise not. Array key[] is used to store key values of all vertices. Another array parent[] to store indexes of parent nodes in MST. The parent array is the output array which is used to show the constructed MST.
- C/C++
- Java
// A C / C++ program for Prim's Minimum Spanning Tree (MST) algorithm.
// The program is for adjacency matrix representation of the graph
#include <stdio.h>
#include <limits.h>
// Number of vertices in the graph
#define V 5
// A utility function to find the vertex with minimum key value, from
// the set of vertices not yet included in MST
int minKey(int key[], bool mstSet[])
{
// Initialize min value
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++)
if (mstSet[v] == false && key[v] < min)
min = key[v], min_index = v;
return min_index;
}
// A utility function to print the constructed MST stored in parent[]
int printMST(int parent[], int n, int graph[V][V])
{
printf("Edge Weight\n");
for (int i = 1; i < V; i++)
printf("%d - %d %d \n", parent[i], i, graph[i][parent[i]]);
}
// Function to construct and print MST for a graph represented using adjacency
// matrix representation
void primMST(int graph[V][V])
{
int parent[V]; // Array to store constructed MST
int key[V]; // Key values used to pick minimum weight edge in cut
bool mstSet[V]; // To represent set of vertices not yet included in MST
// Initialize all keys as INFINITE
for (int i = 0; i < V; i++)
key[i] = INT_MAX, mstSet[i] = false;
// Always include first 1st vertex in MST.
key[0] = 0; // Make key 0 so that this vertex is picked as first vertex
parent[0] = -1; // First node is always root of MST
// The MST will have V vertices
for (int count = 0; count < V-1; count++)
{
// Pick the minimum key vertex from the set of vertices
// not yet included in MST
int u = minKey(key, mstSet);
// Add the picked vertex to the MST Set
mstSet[u] = true;
// Update key value and parent index of the adjacent vertices of
// the picked vertex. Consider only those vertices which are not yet
// included in MST
for (int v = 0; v < V; v++)
// graph[u][v] is non zero only for adjacent vertices of m
// mstSet[v] is false for vertices not yet included in MST
// Update the key only if graph[u][v] is smaller than key[v]
if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v])
parent[v] = u, key[v] = graph[u][v];
}
// print the constructed MST
printMST(parent, V, graph);
}
// driver program to test above function
int main()
{
/* Let us create the following graph
2 3
(0)--(1)--(2)
| / \ |
6| 8/ \5 |7
| / \ |
(3)-------(4)
9 */
int graph[V][V] = {{0, 2, 0, 6, 0},
{2, 0, 3, 8, 5},
{0, 3, 0, 0, 7},
{6, 8, 0, 0, 9},
{0, 5, 7, 9, 0},
};
// Print the solution
primMST(graph);
return 0;
}
Output:Edge Weight
0 - 1 2
1 - 2 3
0 - 3 6
1 - 4 5
Time Complexity of the above program is O(V^2). If the input graph is represented using adjacency list, then the time complexity of Prim’s algorithm can be reduced to O(E log V) with the help of binary heap.
[http://www.geeksforgeeks.org/greedy-algorithms-set-5-prims-minimum-spanning-tree-mst-2/]
END OF UNIT I
No comments:
Post a Comment