Design And Analysis of Algorithms 3

greedy = having an excessive desire or appetite for food.
                             =       having or showing an intense and selfish desire for wealth or power.

Unit - IPart 3

Greedy algorithm

A greedy algorithm is an algorithmic paradigm that follows the problem solving heuristic of making the locally optimal choice at each stage^[1] with the hope of finding a global optimum. In many problems, a greedy strategy does not in general produce an optimal solution, but nonetheless a greedy heuristic may yield locally optimal solutions that approximate a global optimal solution in a reasonable time.

For example, a greedy strategy for the traveling salesman problem (which is of a high computational complexity) is the following heuristic: "At each stage visit an unvisited city nearest to the current city". This heuristic need not find a best solution, but terminates in a reasonable number of steps; finding an optimal solution typically requires unreasonably many steps. In mathematical optimization, greedy algorithms solve combinatorial problems having the properties of matroids.

Specifics[edit]

In general, greedy algorithms have five components:

1. A candidate set, from which a solution is created
2. A selection function, which chooses the best candidate to be added to the solution
3. A feasibility function, that is used to determine if a candidate can be used to contribute to a solution
4. An objective function, which assigns a value to a solution, or a partial solution, and
5. A solution function, which will indicate when we have discovered a complete solution

Greedy algorithms produce good solutions on some mathematical problems, but not on others. Most problems for which they work will have two properties:

Greedy choice property 

We can make whatever choice seems best at the moment and then solve the subproblems that arise later. The choice made by a greedy algorithm may depend on choices made so far, but not on future choices or all the solutions to the subproblem. It iteratively makes one greedy choice after another, reducing each given problem into a smaller one. In other words, a greedy algorithm never reconsiders its choices. This is the main difference from dynamic programming, which is exhaustive and is guaranteed to find the solution.

After every stage, dynamic programming makes decisions based on all the decisions made in the previous stage, and may reconsider the previous stage's algorithmic path to solution.

Optimal substructure 

"A problem exhibits optimal substructure if an optimal solution to the problem contains optimal solutions to the sub-problems."^[2]

Cases of failure[edit]

Examples on how a greedy algorithm may fail to achieve the optimal solution.

Starting at A, a greedy algorithm will find the local maximum at "m", oblivious to the global maximum at "M".

With a goal of reaching the largest-sum, at each step, the greedy algorithm will choose what appears to be the optimal immediate choice, so it will choose 12 instead of 3 at the second step, and will not reach the best solution, which contains 99.

For many other problems, greedy algorithms fail to produce the optimal solution, and may even produce the unique worst possible solution. One example is the traveling salesman problem mentioned above: for each number of cities, there is an assignment of distances between the cities for which the nearest neighbor heuristic produces the unique worst possible tour.^[3]

Types[edit]

Greedy algorithms can be characterized as being 'short sighted', and also as 'non-recoverable'. They are ideal only for problems which have 'optimal substructure'. Despite this, for many simple problems (e.g. giving change), the best suited algorithms are greedy algorithms. It is important, however, to note that the greedy algorithm can be used as a selection algorithm to prioritize options within a search, or branch-and-bound algorithm. There are a few variations to the greedy algorithm:

• Pure greedy algorithms
• Orthogonal greedy algorithms
• Relaxed greedy algorithms

Applications

Greedy algorithms mostly (but not always) fail to find the globally optimal solution, because they usually do not operate exhaustively on all the data. They can make commitments to certain choices too early which prevent them from finding the best overall solution later. For example, all known greedy coloring algorithms for the graph coloring problem and all other NP-complete problems do not consistently find optimum solutions. Nevertheless, they are useful because they are quick to think up and often give good approximations to the optimum.

If a greedy algorithm can be proven to yield the global optimum for a given problem class, it typically becomes the method of choice because it is faster than other optimization methods like dynamic programming. Examples of such greedy algorithms are Kruskal's algorithm and Prim's algorithm for finding minimum spanning trees, and the algorithm for finding optimum Huffman trees.

The theory of matroids, and the more general theory of greedoids, provide whole classes of such algorithms.

Greedy algorithms appear in network routing as well. Using greedy routing, a message is forwarded to the neighboring node which is "closest" to the destination. The notion of a node's location (and hence "closeness") may be determined by its physical location, as in geographic routing used by ad hoc networks. Location may also be an entirely artificial construct as in small world routing and distributed hash table.

Examples

• The activity selection problem is characteristic to this class of problems, where the goal is to pick the maximum number of activities that do not clash with each other.
• In the Macintosh computer game Crystal Quest the objective is to collect crystals, in a fashion similar to the travelling salesman problem. The game has a demo mode, where the game uses a greedy algorithm to go to every crystal. The artificial intelligence does not account for obstacles, so the demo mode often ends quickly.
• The matching pursuit is an example of greedy algorithm applied on signal approximation.
• A greedy algorithm finds the optimal solution to Malfatti's problem of finding three disjoint circles within a given triangle that maximize the total area of the circles; it is conjectured that the same greedy algorithm is optimal for any number of circles.
• A greedy algorithm is used to construct a Huffman tree during Huffman coding where it finds an optimal solution.
• In decision tree learning, greedy algorithms are commonly used, however they are not guaranteed to find the optimal solution.

[https://en.wikipedia.org/wiki/Greedy_algorithm]

Greedy algorithms have some advantages and disadvantages:

1. It is quite easy to come up with a greedy algorithm (or even multiple greedy algorithms) for a problem.
2. Analyzing the run time for greedy algorithms will generally be much easier than for other techniques (like Divide and Conquer). For Divide and Conquer, it is quite unclear whether they are fast or slow because at each level of recursion, on one hand the size of problem is getting smaller and on the other hand the number of subproblems is increasing.
3. The difficult part is that one have to work much harder to understand correctness issues for greedy algorithms. Even with the correct algorithm it's hard to prove why it is correct. Proving that a greedy algorithm is correct is more of an art than science.

[https://www.hackerearth.com/practice/algorithms/greedy/basics-of-greedy-algorithms/tutorial/]

Elements of the Greedy Strategy

Optimal Substructure:

An optimal solution to the  problem contains within it optimal solutions to sub-problems. A' = A - {1} (greedy choice) A' can be solved again with the greedy algorithm. S' = { i Î S, s_i ³  f_i }

When do you use DP versus a greedy approach? Which should be faster?

The 0 - 1 knapsack problem:

A thief has a knapsack that holds at most W pounds. Item i : ( v_i, w_i ) ( v = value, w = weight ) thief must  choose items to maximize the value stolen and still fit into the knapsack. Each item must be taken or left ( 0 - 1 ).

Fractional knapsack problem:

takes parts, as well as wholes

Both the 0 - 1 and fractional problems have the optimal substructure property: Fractional:  v_i / w_i is the value per pound. Clearly you take as much of the item with the greatest value per pound. This continues until you fill the knapsack. Optimal (Greedy) algorithm takes O ( n lg n ), as we must sort on v_i / w_i = d_i.

Consider the same strategy for the 0 - 1 problem:

W = 50 lbs. (maximum knapsack capacity)

w1 = 10	v1 = 60	d1.= 6
w2 = 20	v2 = 100	d2.= 5
w3 = 30	v3 = 120	d3 = 4

were d is the value densityGreedy approach: Take all of 1, and all of 2: v₁+ v₂ = 160, optimal solution is to take all of 2 and 3:  v₂ + v₃= 220, other solution is to take all of 1 and 3 v₁+ v₃ = 180. All below 50 lbs.
When solving the 0 - 1 knapsack problem, empty space lowers the effective d of the load. Thus each time an item is chosen for inclusion we must consider both

• i included
• i excluded

These are clearly overlapping sub-problems for different i's and so best solved by DP!

 [http://www.cs.fsu.edu/~burmeste/slideshow/chapter17/17-2.html]

Knapsack problem

The knapsack problem or rucksack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible. It derives its name from the problem faced by someone who is constrained by a fixed-size knapsack and must fill it with the most valuable items.

The problem often arises in resource allocation where there are financial constraints and is studied in fields such as combinatorics, computer science, complexity theory, cryptography, applied mathematics, and daily fantasy sports.

The knapsack problem has been studied for more than a century, with early works dating as far back as 1897.^[1] The name "knapsack problem" dates back to the early works of mathematician Tobias Dantzig (1884–1956),^[2] and refers to the commonplace problem of packing your most valuable or useful items without overloading your luggage.

Definition[edit]

The most common problem being solved is the 0-1 knapsack problem, which restricts the number x_i of copies of each kind of item to zero or one. Given a set of n items numbered from 1 up to n, each with a weight w_i and a value v_i, along with a maximum weight capacity W,

maximize ${\displaystyle \sum _{i=1}^{n}v_{i}x_{i}}$

subject to ${\displaystyle \sum _{i=1}^{n}w_{i}x_{i}\leq W}$ and ${\displaystyle x_{i}\in \{0,1\}}$.

Here x_i represents the number of instances of item i to include in the knapsack. Informally, the problem is to maximize the sum of the values of the items in the knapsack so that the sum of the weights is less than or equal to the knapsack's capacity.

The bounded knapsack problem (BKP) removes the restriction that there is only one of each item, but restricts the number ${\displaystyle x_{i}}$ of copies of each kind of item to a maximum non-negative integer value ${\displaystyle c}$:

maximize ${\displaystyle \sum _{i=1}^{n}v_{i}x_{i}}$

subject to ${\displaystyle \sum _{i=1}^{n}w_{i}x_{i}\leq W}$ and ${\displaystyle 0\leq x_{i}\leq c}$

The unbounded knapsack problem (UKP) places no upper bound on the number of copies of each kind of item and can be formulated as above except for that the only restriction on ${\displaystyle x_{i}}$ is that it is a non-negative integer.

maximize ${\displaystyle \sum _{i=1}^{n}v_{i}x_{i}}$

subject to ${\displaystyle \sum _{i=1}^{n}w_{i}x_{i}\leq W}$ and ${\displaystyle x_{i}\geq 0}$

One example of the unbounded knapsack problem is given using the figure shown at the beginning of this article and the text "if any number of each box is available" in the caption of that figure.

Computational complexity[edit]

The knapsack problem is interesting from the perspective of computer science for many reasons:

• The decision problem form of the knapsack problem (Can a value of at least V be achieved without exceeding the weight W?) is NP-complete, thus there is no known algorithm both correct and fast (polynomial-time) on all cases.
• While the decision problem is NP-complete, the optimization problem is NP-hard, its resolution is at least as difficult as the decision problem, and there is no known polynomial algorithm which can tell, given a solution, whether it is optimal (which would mean that there is no solution with a larger V, thus solving the NP-complete decision problem).
• There is a pseudo-polynomial time algorithm using dynamic programming.
• There is a fully polynomial-time approximation scheme, which uses the pseudo-polynomial time algorithm as a subroutine, described below.
• Many cases that arise in practice, and "random instances" from some distributions, can nonetheless be solved exactly.

There is a link between the "decision" and "optimization" problems in that if there exists a polynomial algorithm that solves the "decision" problem, then one can find the maximum value for the optimization problem in polynomial time by applying this algorithm iteratively while increasing the value of k . On the other hand, if an algorithm finds the optimal value of optimization problem in polynomial time, then the decision problem can be solved in polynomial time by comparing the value of the solution output by this algorithm with the value of k . Thus, both versions of the problem are of similar difficulty.

One theme in research literature is to identify what the "hard" instances of the knapsack problem look like,^[9][10] or viewed another way, to identify what properties of instances in practice might make them more amenable than their worst-case NP-complete behaviour suggests.^[11] The goal in finding these "hard" instances is for their use in public key cryptography systems, such as the Merkle-Hellman knapsack cryptosystem.

Solving[edit]

Several algorithms are available to solve knapsack problems, based on dynamic programming approach,^[12] branch and bound approach^[13] or hybridizations of both approaches.^{[11][14][15][16]}

Dynamic programming in-advance algorithm[edit]

Unbounded knapsack problem[edit]

If all weights (${\displaystyle w_{1},\ldots ,w_{n}}$) are nonnegative integers, the knapsack problem can be solved in pseudo-polynomial time using dynamic programming. The following describes a dynamic programming solution for the unbounded knapsack problem.

To simplify things, assume all weights are strictly positive (${\displaystyle w_{i}>0}$). We wish to maximize total value subject to the constraint that total weight is less than or equal to ${\displaystyle W}$. Then for each ${\displaystyle w\leq W}$, define ${\displaystyle m[w]}$ to be the maximum value that can be attained with total weight less than or equal to ${\displaystyle w}$. Then, ${\displaystyle m[W]}$ is the solution to the problem.

Observe that ${\displaystyle m[w]}$ has the following properties:

• ${\displaystyle m[0]=0\,\!}$ (the sum of zero items, i.e., the summation of the empty set)
• ${\displaystyle m[w]=\max _{w_{i}\leq w}(v_{i}+m[w-w_{i}])}$

where ${\displaystyle v_{i}}$ is the value of the i-th kind of item.

(To formulate the equation above, the idea used is that the solution for a knapsack is the same as the value of one correct item plus the solution for a knapsack with smaller capacity, specifically one with the capacity reduced by the weight of that chosen item.)

Here the maximum of the empty set is taken to be zero. Tabulating the results from ${\displaystyle m[0]}$ up through ${\displaystyle m[W]}$ gives the solution. Since the calculation of each ${\displaystyle m[w]}$ involves examining ${\displaystyle n}$ items, and there are ${\displaystyle W}$ values of ${\displaystyle m[w]}$ to calculate, the running time of the dynamic programming solution is ${\displaystyle O(nW)}$. Dividing ${\displaystyle w_{1},\,w_{2},\,\ldots ,\,w_{n},\,W}$ by their greatest common divisor is a way to improve the running time.

The ${\displaystyle O(nW)}$ complexity does not contradict the fact that the knapsack problem is NP-complete, since ${\displaystyle W}$, unlike ${\displaystyle n}$, is not polynomial in the length of the input to the problem. The length of the ${\displaystyle W}$ input to the problem is proportional to the number of bits in ${\displaystyle W}$, ${\displaystyle \log W}$, not to ${\displaystyle W}$ itself.

0/1 knapsack problem[edit]

A similar dynamic programming solution for the 0/1 knapsack problem also runs in pseudo-polynomial time. Assume ${\displaystyle w_{1},\,w_{2},\,\ldots ,\,w_{n},\,W}$ are strictly positive integers. Define ${\displaystyle m[i,w]}$ to be the maximum value that can be attained with weight less than or equal to ${\displaystyle w}$ using items up to ${\displaystyle i}$ (first ${\displaystyle i}$ items).

We can define ${\displaystyle m[i,w]}$ recursively as follows:

• ${\displaystyle m[0,\,w]=0}$
• ${\displaystyle m[i,\,w]=m[i-1,\,w]}$ if ${\displaystyle w_{i}>w\,\!}$ (the new item is more than the current weight limit)
• ${\displaystyle m[i,\,w]=\max(m[i-1,\,w],\,m[i-1,w-w_{i}]+v_{i})}$ if ${\displaystyle w_{i}\leqslant w}$.

The solution can then be found by calculating ${\displaystyle m[n,W]}$. To do this efficiently we can use a table to store previous computations.

The following is pseudo code for the dynamic program:

 1 // Input:
 2 // Values (stored in array v)
 3 // Weights (stored in array w)
 4 // Number of distinct items (n)
 5 // Knapsack capacity (W)
 6 
 7 for j from 0 to W do:
 8     m[0, j] := 0
 9 
10 for i from 1 to n do:
11     for j from 0 to W do:
12         if w[i] > j then:
13             m[i, j] := m[i-1, j]
14         else:
15             m[i, j] := max(m[i-1, j], m[i-1, j-w[i]] + v[i])

This solution will therefore run in ${\displaystyle O(nW)}$ time and ${\displaystyle O(nW)}$ space. Additionally, if we use only a 1-dimensional array ${\displaystyle m[w]}$ to store the current optimal values and pass over this array ${\displaystyle i+1}$ times, rewriting from ${\displaystyle m[W]}$ to ${\displaystyle m[1]}$ every time, we get the same result for only ${\displaystyle O(W)}$ space.^{[citation needed]}

Meet-in-the-middle[edit]

Another algorithm for 0-1 knapsack, discovered in 1974 ^[17] and sometimes called "meet-in-the-middle" due to parallels to a similarly named algorithm in cryptography, is exponential in the number of different items but may be preferable to the DP algorithm when ${\displaystyle W}$ is large compared to n. In particular, if the ${\displaystyle w_{i}}$ are nonnegative but not integers, we could still use the dynamic programming algorithm by scaling and rounding (i.e. using fixed-point arithmetic), but if the problem requires ${\displaystyle d}$ fractional digits of precision to arrive at the correct answer, ${\displaystyle W}$ will need to be scaled by ${\displaystyle 10^{d}}$, and the DP algorithm will require ${\displaystyle O(W10^{d})}$ space and ${\displaystyle O(nW10^{d})}$ time.

Meet-in-the-middle algorithm

  input: 
    a set of items with weights and values
  output: 
    the greatest combined value of a subset
  partition the set {1...n} into two sets A and B of approximately equal size
  compute the weights and values of all subsets of each set
  for each subset of A
    find the subset of B of greatest value such that the combined weight is less than W
  keep track of the greatest combined value seen so far

The algorithm takes ${\displaystyle O(2^{n/2})}$ space, and efficient implementations of step 3 (for instance, sorting the subsets of B by weight, discarding subsets of B which weigh more than other subsets of B of greater or equal value, and using binary search to find the best match) result in a runtime of ${\displaystyle O(n2^{n/2})}$. As with the meet in the middle attack in cryptography, this improves on the ${\displaystyle O(n*2^{n})}$ runtime of a naive brute force approach (examining all subsets of {1...n}), at the cost of using exponential rather than constant space (see also baby-step giant-step).

Approximation algorithms[edit]

As for most NP-complete problems, it may be enough to find workable solutions even if they are not optimal. Preferably, however, the approximation comes with a guarantee on the difference between the value of the solution found and the value of the optimal solution.

As with many useful but computationally complex algorithms, there has been substantial research on creating and analyzing algorithms that approximate a solution. The knapsack problem, though NP-Hard, is one of a collection of algorithms that can still be approximated to any specified degree. This means that the problem has a polynomial time approximation scheme. To be exact, the knapsack problem has a fully polynomial time approximation scheme (FPTAS).^[18]

Greedy approximation algorithm[edit]

George Dantzig proposed a greedy approximation algorithm to solve the unbounded knapsack problem.^[19] His version sorts the items in decreasing order of value per unit of weight, ${\displaystyle v_{i}/w_{i}}$. It then proceeds to insert them into the sack, starting with as many copies as possible of the first kind of item until there is no longer space in the sack for more. Provided that there is an unlimited supply of each kind of item, if ${\displaystyle m}$ is the maximum value of items that fit into the sack, then the greedy algorithm is guaranteed to achieve at least a value of ${\displaystyle m/2}$. However, for the bounded problem, where the supply of each kind of item is limited, the algorithm may be far from optimal.

Fully polynomial time approximation scheme[edit]

The fully polynomial time approximation scheme (FPTAS) for the knapsack problem takes advantage of the fact that the reason the problem has no known polynomial time solutions is because the profits associated with the items are not restricted. If one rounds off some of the least significant digits of the profit values then they will be bounded by a polynomial and 1/ε where ε is a bound on the correctness of the solution. This restriction then means that an algorithm can find a solution in polynomial time that is correct within a factor of (1-ε) of the optimal solution.^[18]

An Algorithm for FPTAS

 input: 
   ε ∈ [0,1]
   a list A of n items, specified by their values, ${\displaystyle v_{i}}$, and weights
 output:
   S' the FPTAS solution

 P := max ${\displaystyle \{v_{i}\mid 1\leq i\leq n\}}$  // the highest item value
 K := ε ${\displaystyle {\frac {P}{n}}}$
 for i from 1 to n do
    ${\displaystyle v'_{i}}$ := ${\displaystyle \left\lfloor {\frac {v_{i}}{K}}\right\rfloor }$
 end for
 return the solution, S', using the ${\displaystyle v'_{i}}$ values in the dynamic program outlined above

Theorem: The set ${\displaystyle S'}$ computed by the algorithm above satisfies ${\displaystyle \mathrm {profit} (S')\geq (1-\varepsilon )\cdot \mathrm {profit} (S^{*})}$, where ${\displaystyle S^{*}}$ is an optimal solution.

Dominance relations[edit]

Solving the unbounded knapsack problem can be made easier by throwing away items which will never be needed. For a given item i, suppose we could find a set of items J such that their total weight is less than the weight of i, and their total value is greater than the value of i. Then i cannot appear in the optimal solution, because we could always improve any potential solution containing i by replacing i with the set J. Therefore, we can disregard the i-th item altogether. In such cases, J is said to dominate i. (Note that this does not apply to bounded knapsack problems, since we may have already used up the items in J.)

Finding dominance relations allows us to significantly reduce the size of the search space. There are several different types of dominance relations,^[11] which all satisfy an inequality of the form:

${\displaystyle \qquad \sum _{j\in J}w_{j}\,x_{j}\ \leq \alpha \,w_{i}}$, and ${\displaystyle \sum _{j\in J}v_{j}\,x_{j}\ \geq \alpha \,v_{i}\,}$ for some ${\displaystyle x\in Z_{+}^{n}}$

where ${\displaystyle \alpha \in Z_{+}\,,J\subsetneq N}$ and ${\displaystyle i\not \in J}$. The vector ${\displaystyle x}$ denotes the number of copies of each member of J.

Collective dominance

The i-th item is collectively dominated by J, written as ${\displaystyle i\ll J}$, if the total weight of some combination of items in J is less than w_i and their total value is greater than v_i. Formally, ${\displaystyle \sum _{j\in J}w_{j}\,x_{j}\ \leq w_{i}}$ and ${\displaystyle \sum _{j\in J}v_{j}\,x_{j}\ \geq v_{i}}$ for some ${\displaystyle x\in Z_{+}^{n}}$, i.e. ${\displaystyle \alpha =1}$. Verifying this dominance is computationally hard, so it can only be used with a dynamic programming approach. In fact, this is equivalent to solving a smaller knapsack decision problem where ${\displaystyle V=v_{i}}$, ${\displaystyle W=w_{i}}$, and the items are restricted to J.

Threshold dominance

The i-th item is threshold dominated by J, written as ${\displaystyle i\prec \prec J}$, if some number of copies of ${\displaystyle i}$ are dominated by J. Formally, ${\displaystyle \sum _{j\in J}w_{j}\,x_{j}\ \leq \alpha \,w_{i}}$, and ${\displaystyle \sum _{j\in J}v_{j}\,x_{j}\ \geq \alpha \,v_{i}\,}$ for some ${\displaystyle x\in Z_{+}^{n}}$ and ${\displaystyle \alpha \geq 1}$. This is a generalization of collective dominance, first introduced in^[12] and used in the EDUK algorithm. The smallest such ${\displaystyle \alpha }$ defines the threshold of the item ${\displaystyle i}$, written ${\displaystyle t_{i}=(\alpha -1)w_{i}}$. In this case, the optimal solution could contain at most ${\displaystyle \alpha -1}$ copies of ${\displaystyle i}$.

Multiple dominance

The i-th item is multiply dominated by a single item ${\displaystyle j}$, written as ${\displaystyle i\ll _{m}j}$, if ${\displaystyle i}$ is dominated by some number of copies of ${\displaystyle j}$. Formally, ${\displaystyle w_{j}\,x_{j}\ \leq w_{i}}$, and ${\displaystyle v_{j}\,x_{j}\ \geq v_{i}}$ for some ${\displaystyle x_{j}\in Z_{+}}$ i.e. ${\displaystyle J=\{j\},\alpha =1,x_{j}=\lfloor {\frac {w_{i}}{w_{j}}}\rfloor }$. This dominance could be efficiently used during preprocessing because it can be detected relatively easily.

Modular dominance

Let b be the best item, i.e. ${\displaystyle {\frac {v_{b}}{w_{b}}}\geq {\frac {v_{i}}{w_{i}}}\,}$ for all ${\displaystyle i}$. This is the item with the greatest density of value. The i-th item is modularly dominated by a single item ${\displaystyle j}$, written as ${\displaystyle i\ll _{\equiv }j}$, if ${\displaystyle i}$ is dominated by ${\displaystyle j}$ plus several copies of b. Formally, ${\displaystyle w_{j}+tw_{b}\leq w_{i}}$, and ${\displaystyle v_{j}+tv_{b}\geq v_{i}}$ i.e. ${\displaystyle J=\{b,j\},\alpha =1,x_{b}=t,x_{j}=1}$.

Variations[edit]

There are many variations of the knapsack problem that have arisen from the vast number of applications of the basic problem. The main variations occur by changing the number of some problem parameter such as the number of items, number of objectives, or even the number of knapsacks.

Multi-objective knapsack problem[edit]

This variation changes the goal of the individual filling the knapsack. Instead of one objective, such as maximizing the monetary profit, the objective could have several dimensions. For example, there could be environmental or social concerns as well as economic goals. Problems frequently addressed include portfolio and transportation logistics optimizations.^[20][21]

As a concrete example, suppose you ran a cruise ship. You have to decide how many famous comedians to hire. This boat can handle no more than one ton of passengers and the entertainers must weigh less than 1000 lbs. Each comedian has a weight, brings in business based on their popularity and asks for a specific salary. In this example you have multiple objectives. You want, of course, to maximize the popularity of your entertainers while minimizing their salaries. Also, you want to have as many entertainers as possible.

Multi-dimensional knapsack problem[edit]

In this variation, the weight of knapsack item ${\displaystyle i}$ is given by a D-dimensional vector ${\displaystyle {\overline {w_{i}}}=(w_{i1},\ldots ,w_{iD})}$ and the knapsack has a D-dimensional capacity vector ${\displaystyle (W_{1},\ldots ,W_{D})}$. The target is to maximize the sum of the values of the items in the knapsack so that the sum of weights in each dimension ${\displaystyle d}$ does not exceed ${\displaystyle W_{d}}$.

Multi-dimensional knapsack is computationally harder than knapsack; even for ${\displaystyle D=2}$, the problem does not have EPTAS unless P${\displaystyle =}$NP.^[22] However, the algorithm in ^[23] is shown to solve sparse instances efficiently. An instance of multi-dimensional knapsack is sparse if there is a set ${\displaystyle J=\{1,2,\ldots ,m\}}$ for ${\displaystyle m<D}$ such that for every knapsack item ${\displaystyle i}$, ${\displaystyle \exists z>m}$ such that ${\displaystyle \forall j\in J\cup \{z\},\ w_{ij}\geq 0}$ and ${\displaystyle \forall y\notin J\cup \{z\},w_{iy}=0}$. Such instances occur, for example, when scheduling packets in a wireless network with relay nodes.^[23] The algorithm from ^[23] also solves sparse instances of the multiple choice variant, multiple-choice multi-dimensional knapsack.

The IHS (Increasing Height Shelf) algorithm is optimal for 2D knapsack (packing squares into a two-dimensional unit size square): when there are at most five square in an optimal packing.^[24]

Multiple knapsack problem[edit]

This variation is similar to the Bin Packing Problem. It differs from the Bin Packing Problem in that a subset of items can be selected, whereas, in the Bin Packing Problem, all items have to be packed to certain bins. The concept is that there are multiple knapsacks. This may seem like a trivial change, but it is not equivalent to adding to the capacity of the initial knapsack. This variation is used in many loading and scheduling problems in Operations Research and has a PTAS^[25]

Quadratic knapsack problem[edit]

As described by Wu et al.:

The quadratic knapsack problem (QKP) maximizes a quadratic objective function subject to a binary and linear capacity constraint.^[26]

The quadratic knapsack problem was discussed under that title by Gallo, Hammer, and Simeone in 1980.^[27] However, Gallo and Simeone^[28] attribute the first treatment of the problem to Witzgall^[29] in 1975.

Subset-sum problem[edit]

The subset sum problem is a special case of the decision and 0-1 problems where each kind of item, the weight equals the value: ${\displaystyle w_{i}=v_{i}}$. In the field of cryptography, the term knapsack problem is often used to refer specifically to the subset sum problem and is commonly known as one of Karp's 21 NP-complete problems.^[30]

The generalization of subset sum problem is called multiple subset-sum problem, in which multiple bins exist with the same capacity. It has been shown that the generalization does not have an FPTAS.^[31]

[https://en.wikipedia.org/wiki/Knapsack_problem]

Kinds of Knapsack Problems

• Two main kinds of Knapsack Problems:
1. 0-1 Knapsack:
• N items (can be the same or different)
• Have only one of each
• Must leave or take (ie 0-1) each item (eg ingots of gold)
• DP works, greedy does not


2. Fractional Knapsack:
• N items (can be the same or different)
• Can take fractional part of each item (eg bags of gold dust)
• Greedy works and DP algorithms work


• Knapsack Problem that we did earlier with DP:
• N kinds of items
• Have unlimited supply of each item
• Equivalent to a 0-1 problem in which there are enough of each item to fill the knapsack

---

Fractional Knapsack: Greedy Solution

• Algorithm:
• Assume knapsack holds weight W and items have value v_i and weight w_i
• Rank items by value/weight ratio: v_i / w_i
• Thus: v_i / w_i ≥ v_j / w_j, for all i ≤ j
• Consider items in order of decreasing ratio
• Take as much of each item as possible


• Code:

    -- Assumes value and weight arrays are sorted by vi/wi
    Fractional-Knapsack(v, w, W)
        load := 0
        i := 1
        while load < W and i ≤ n loop
            if wi ≤ W - load then
                take all of item i
            else
                take (W-load) / wi of item i
            end if
            add weight of what was taken to load
            i := i + 1
        end loop
        return load
    

• Example: Knapsack Capacity W = 30 and

  Item	A	B	C	D
  Value	50	140	60	60
  Size	5	20	10	12
  Ratio	10	7	6	5

• Solution:
• All of A, all of B, and ((30-25)/10) of C (and none of D)
• Size: 5 + 20 + 10*(5/10) = 30
• Value: 50 + 140 + 60*(5/10) = 190 + 30 = 220


• Time: Θ(n), if already sorted

---

Greedy Algorithms Don't Work for 0-1 Knapsack Problems

• Greedy doesn't work for 0-1 Knapsack Problem:
• Example 1: Knapsack Capacity W = 25 and

  Item	A	B	C	D
  Price	12	9	9	5
  Size	24	10	10	7



• Optimal: B and C. Size=10+10=20. Price=9+9=18
• Possible greedy approach: take largest Price first (Price=12, not optimal)
• Possible greedy approach: take smallest size item first (Price=9+5=14, not optimal)


• Example 2: Knapsack Capacity = 30

Item	A	B	C
Price	50	140	60
Size	5	20	10
Ratio	10	7	6



• Possible greedy approach: take largest ratio: (Solution: A and B. Size=5+20=25. Price=50+140=190


• Optimal: B and C. Size=20+10=30. Price=140+60=200


• Greedy fractional: A, B, and half of C. Size=5+20+10*(5/10)=30. Price 50+140+60*(5/10) = 190+30 = 220


• For comparison: DP algorithm gives 18
• Use 2D array: rows 0..25, columns 0..4
• Initialize first row and column to 0
• Solve a row at a time, subtracting off added size as needed
• What is the best way to fill:
• With A only: sizes 0..23, 24, 25
• With A,B only: sizes 0..9, 10, 11..23, 24, 25
• With A,B,C only: sizes 0..9, 10, 11..19, 20, 21..23, 24, 25
• With A,B,C,D: sizes 0..6, 7, 8..9, 10, 11..16, 17, 18..19, 20, 21..23, 24, 25

---

Greedy vs DP (Overview)

• With DP: solve subproblems first, then use those solutions to make an optimal choice


• With Greedy: make an optimal choice (without knowing solutions to subproblems) and then solve remaining subproblem(s)


• DP solutions are bottom up; greedy are top down


• Both apply to problems with optimal substructure: solution to larger problem contains solutions to (1 or more) subproblems

---

Another Greedy Algorithm: Huffman Coding

• Goal: Compress data


• Assumptions:
• Data are a sequence of characters, encoded with some fixed length scheme
• Frequency of characters is known


• Basic technique: Compress by encoding each character as a specific, variable length bit string


• Key idea: encode common characters with short codewords


• Efficient encoding with a variable length code requires a prefix code

---

Prefix Code

• In a prefix code, no codeword is a prefix of any other codeword
• A codeword is a word in the code
• In the codes below, what are the codewords?
• Is the first code below a prefix code?
• Is the second code below a prefix code?
• No codeword has a prefix of 0, 101, 100, 111, etc


• In a prefix code, you can always (efficiently) determine when one codeword ends and the next begins
• Example: 1011101111011111000101
• Solution: 101 1101 111 0 111 1100 0 101

---

Huffman Coding Example

• Example (from CLRS): encode characters a .. f



character to encode	a	b	c	d	e	f
Frequency	45	13	12	16	9	5
Fixed length codeword	000	001	010	011	100	101
Variable length codeword	0	101	100	111	1101	1100

• Total frequency is 100
• An prefix code that is optimal always exists - but how to find it?

---

Codes as Trees

• The trees below represent the codes above
• The path to a leaf represents the code for the character in that leaf
• Non-leaf node values are total frequencies below

---

Huffman Code Algorithm

• Algorithm idea:
• Build tree from bottom up
• Repeat until 1 tree results: join 2 smallest nodes and update frequencies
• Keep nodes and subtrees on a priority queue to find smallest 2 nodes
• Sort by frequencies of total in tree


• Algorithm:

        -- Assume that Q.front removes and returns the front of the queue
        Huffman(C)
        Q := C
        for i in C.size - 1 loop
            l = Q.front
            r = Q.front
            newFreq := l.freq + r.freq
            n := new Node'(l, r, newFreq)
            Q.insert(n)
        



• Sequence of building tree:
• f,e,c,b,d,a
• c,b,(f,e), d, a
• (f,e), d, (c, b), a
• (c,b), ((f,e), d), a
• a, ((c,b),((f,e), d))
• (a, ((c,b),((f,e), d)))

---

Another Greedy Algorithm: Activity Selection

• Problem:
• Set of n activities that each require exclusive use of a common resource (eg a room)
• S = {a₁, a₂, ..., a_n}, S is a set of activties
• Each a_i needs the resource during period [s_i, f_i)
• a_i needs resource from start time s_i up to but not including finish time f_i
• Objective: Select largest possible set of nonoverlapping (mutually compatible) activities


• Imagine: Spend day at theater. maximize number of films watched.


• Could have other problems: eg longest total time, maximize fees


• Assume S is sorted by finish time (ie f₁ ≤ f₂ ≤ f₃ ≤ ... ≤ f_n-1 ≤ f_n)

---

Example

• Example (from CLRS) - solve for S =

i	1	2	3	4	5	6	7	8	9
si	1	2	4	1	5	8	9	11	13
fi	3	5	7	8	9	10	11	14	16



• A diagram:

            :a5-----.
    :a4-----------.
      :a2---.       :a7-.   :a9---.             
    :a1-. :a3---. :a6-. :a8---.                                  
    + + + + + + + + + + + + + + + +
    1-2-3-4-5-6-7-8-9-0-1-2-3-4-5-6
    

• Two maximal solutions: {a₁, a₃, a₆, a₈}, and {a₂, a₅, a₇, a₉}

---

Optimal Substructure

• Define S_ij
• S_ij = activities that start after a_i finishes and finish before a_j starts
• S_ij = activities can be done between a_i and a_j
• S_ij = {a_k ∈ S | f_i ≤ s_k < f_k ≤ s_j }
• Diagram: -ai-: :-ak-: :-aj---
• S₁₈ = {a₃, a₅, a₆, a₇}


• Let A_ij = an optimal solution to S_ij
• eg A₁₈ = {a₃, a₆}


• Choose any activity a_k ∈ A_ij. It defines two subproblems:
1. Solve S_ik
2. Solve S_kj
3. Example: choose a₃ ∈ A₁₈, which gives subproblems S₁₃ = {} and S₃₈ = {a₆, a₇}


• Now let's use a_k, to define A_ik and A_kj and then show that they are optimal:
• Let A_ik = A_ij ∩ S_ik; eg choose a₃, A₁₃ = {}
• Let A_kj = A_ij ∩ S_kj eg choose a₃, A₃₈ = {a₆}
• Now A_ij = A_ik ∪ {a_k} ∪ A_kj
• and thus |A_ij| = |A_ik| + 1 + |A_kj|
• But, A_ij is optimal, and so A_ik and A_kj must also be optimal
• Otherwise we could cut and paste and improve A_ij


• The provides a basis for a recursive solution

---

DP Solutions

• Proved above: Optimal solution A_ij contains optimal solutions for S_ik and S_kj. This gives the following:
• Let c(i, j) = size of optimal solution for S_ij
• Then c(i, j) = c(i, k) + 1 + c(k, j), for some a_k


• To find the right activity $a_k$ to choose, we try them all:


$ \displaystyle c(i, j) = \begin{cases} & 0, \text{if }S_{ij} = \emptyset \\ & \max_{a_k \in S_{ij}}\{c(i,k) + 1 + c(k,j)\}, \text{if }S_{ij} \ne \emptyset \end{cases} $


• We could implement this top down or bottom up. What would the table look like?
• The DP solution tries all subproblems. Can we find a Greedy solution?

---

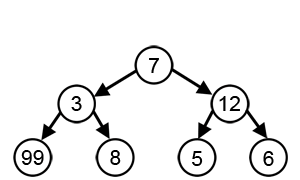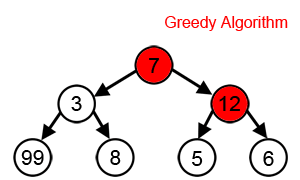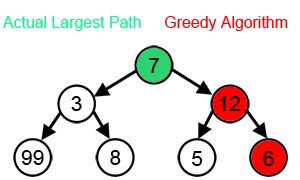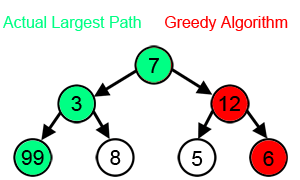
A Greedy Solution

• Don't need dynamic programming - greedy solution works


• Greedy Approach: choose activity to add to optimal solution before solving subproblems!


• Which activity to add: the one that leaves the most time for others
• Which leaves the most time: the first to finish!
• ie a₁


• After choosing first to finish, only one subproblem remains
• And it is solved by the same method


• Algorithm:
• Choose activity that finishes first
• Throw out activities that start before the chosen one finishes
• Repeat until done


• Let's try it:

            :a5-----.
    :a4-----------.
      :a2---.       :a7-.   :a9---.             
    :a1-. :a3---. :a6-. :a8---.                                  
    + + + + + + + + + + + + + + + +
    1-2-3-4-5-6-7-8-9-0-1-2-3-4-5-6
    

• Add a1, throw out a2, a4
• Add a3, throw out a5
• Add a6, throw out a7
• Add a8, throw out a9

---

Formalizing the Greedy Approach

• Simpler notation for subproblem: S_k = {a_i ∈ S |f_k ≤ s_i }
• In other words, S_k is the set of activities that finish when or after activity a_k finishes


• After choosing a_k to add to solution, we must solve S_k


• If a_k is the first to finish in S_ij, can we guarantee that a_k is part of an optimal solution to S_ij (ie a_k ∈ A_ij for some optimal solution A_ij):
• Let a_k be the earliest finisher in S_ij
• Let a_m ∈ A_ij be the earliest finisher in A_ij
• If k=m then a_k is part of an optimal solution, and we are done.
• If k ≠ m then
• Simply replace a_m with a₁ in the optimal solution
• This must be possible (because both start after a_i, and a_k ends at or before a_m)
• We get a new optimal of the same size!
• Thus choosing a_k can lead to an optimal solution


• We can extend this to all of the S_k

---

Recursive Greedy Solution

• Define a₀ with f₀ = 0 and thus S₀ = S
• Code:

    -- s and f are start and finish arrays 
    -- n activities in original problem
    -- k index of current subproblem
    -- Finds maximal set of activies that start after activity k finishes
    -- Call: RAS(s, f, 0, n)
    Rec-Activity-Selector(s, f, k, n)
        m = k + 1

        -- Find first activity that starts when or after k finishes
        while m ≤ n and s(m) < f(k) loop
            m := m + 1;
        end loop

        if m ≤ n then
            return {am} ∪ Rec-Activity-Selector(s, f, m, n)
        else
            return empty-set
        end if;
    

• Time: Θ(n), if s and f are sorted

---

Iterative Greedy Algorithm

• Code is easy:

    Greedy-Activity-Selector(s, f)
        n := s.length
        A := {a1}  -- Put first activity in maximal
        k := 1
        -- Find next activity to finish
        for m in 2 .. n loop
            if s(m) ≥ f(k) then
                A := A ∪ (am}
                k := m
            end if
        end loop
        return A
    

• Time: Θ(n), if s and f are sorted

---

Greedy vs Dynamic Programming (1)

• DP:
• Choice at each step depends on solutions to subproblems
• Work on subproblems from bottom up
• A memoized recursive solution effectively works from bottom up


• Many subproblems are repeated in solving larger problems
• Example: solving rod cuttin for length 3 uses the solutions for lengths 2, and 1. Solving it for length 4 uses solutions for 3, 2, and 1. Thus, the solutions for 2 and 1 are reused in solving every value larger than 2.
• This repetition results in great savings when the computation is bottom up.


• Greedy:
• Make best choice at current time, then work on subproblems
• Best choice does not depend on solutions to subproblems
• Best choice does depend on choices so far


• Problems solved by both exhibit optimal substructure
• Optimal Substructure: solution to problem contains within it optimal solutions to subproblems


• Key idea: do you have to compare solutions that contain and don't contain the item
• 0-1 Knapsack: to determine whether to include item i for a given size, must consider best solution, at that size, with and without item i
• Fractional knapsack: at each step, choose item with highest ratio


• Proof needed: must show that optimal solution contains greedy solution

---

Greedy vs Dynamic Programming (2)

• We can characterize greedy and dynamic programming solutions, as follows
• Dynamic programming - to find max value for problem P:

    T - a Table of the values of the best solutions of problems of sizes Smallest upto P

    for i in Smallest subproblem to P loop
        T(i) := MAX of:
            T(j) + cost of choice that changes subproblem j into problem i
            T(k) + cost of choice that changes subproblem k into problem i
            ... as many subproblems as needed
    end loop
    Result is T(P) 
    

• T has as many dimensions as needed
• Number of dimensions determined by recursive equation
• Each dimension needs a loop
• Think of T as cached solutions to smaller problems
• We fill T with solutions first to small problems, then to large problems


• Greedy Algorithm - to find maximum value for problem P:

    tempP = P    -- tempP is the remaining subproblem
    while tempP not empty loop
        in subproblem tempP, decide greedy choice C
        Add value of C to solution
        tempP := subproblem tempP reduced based on choice C
    end loop
    

[http://www.radford.edu/~nokie/classes/360/greedy.html]

Job Sequencing

For this Topic Refer following Link
[https://www.academia.edu/8799813/Greedy_Algorithm]